
Q: Is sohcahtoa only for right triangles? A: Yes, it only applies to right triangles. So how do we remember these three trig ratios and use them to solve for missing sides and angles?įinding Sides and Angles Using Inverse Trig Common Questions Remember the three basic ratios are called Sine, Cosine, and Tangent, and they represent the foundational Trigonometric Ratios, after the Greek word for triangle measurement.Īnd these trigonometric ratios allow us to find missing sides of a right triangle, as well as missing angles. Key Point: Regardless of the size of the triangle, these trigonometric ratios will always hold true for right triangles. Therefore, the sets of ratios depend only on the measure of the acute angle, not the size of the triangle. It stated that the ratios of the lengths of two sides of similar right triangles are equal. We’ll dive further into the theory behind it in the video below, but essentially it’s taken from the AA Similarity Postulate that we learned about previously. It’s a mnemonic device to help you remember the three basic trig ratios used to solve for missing sides and angles in a right triangle. It’s probably one of the most famous math mnemonics alongside PEMDAS.Īnd it’s an essential technique for your mathematical toolbelt. This is done using corresponding reference angle in the first quarter as discussed above in the ‘Reference Angles and Trigonometric Functions’ section.Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher) Assume that the original angle is Quadrantġ) Used to find the value of an angle with trigonometric functions such as the sine or cosine value of any angle. Given below is a table showing the values of reference angles in radians and degrees in the four coordinate planes. When calculated in radians: 180° = π, 360° = 2π, 270 = 2π/2, and 90° = π/2Ĭase 1: (For Angles between 0° to 90°) – First quadrantĬase 2: (For Angles between 90° to 180°) – Second quadrantĬase 3: (For Angles between 180° to 270°) – Third quadrantĬase 4: (For Angles between 270° to 360°) – Fourth quadrant So, if the given angle is 310°, then its reference angle is (360° – 310° = 50°). So, if the given angle is 200°, then its reference angle is (200° – 180° = 20°).Ĭase 4: (For Angles between 270° to 360°) – When the terminal side is on the fourth quadrant, the reference angle is 360° minus our given angle. So, if the given angle is 105°, then its reference angle is (180° – 105° = 75°).Ĭase 3: (For Angles between 180° to 270°) – When the terminal side is on the third quadrant, the reference angle is the given angle minus 180°. So, if the given angle is 45°, then its reference angle is also 45°.Ĭase 2: (For Angles between 90° to 180°) – When the terminal side is on the second quadrant, the reference angle is 180° minus our given angle. There are four possible cases:Ĭase 1: (For Angles between 0° to 90°) – When the terminal side is on the first quadrant, the reference angle is the same as the given angle. We can find reference angles depending on which quadrant the terminal side of the angle is located in either degrees or radians.
ALL STUDENTS TAKE CALCULUS MNENOMIC HOW TO
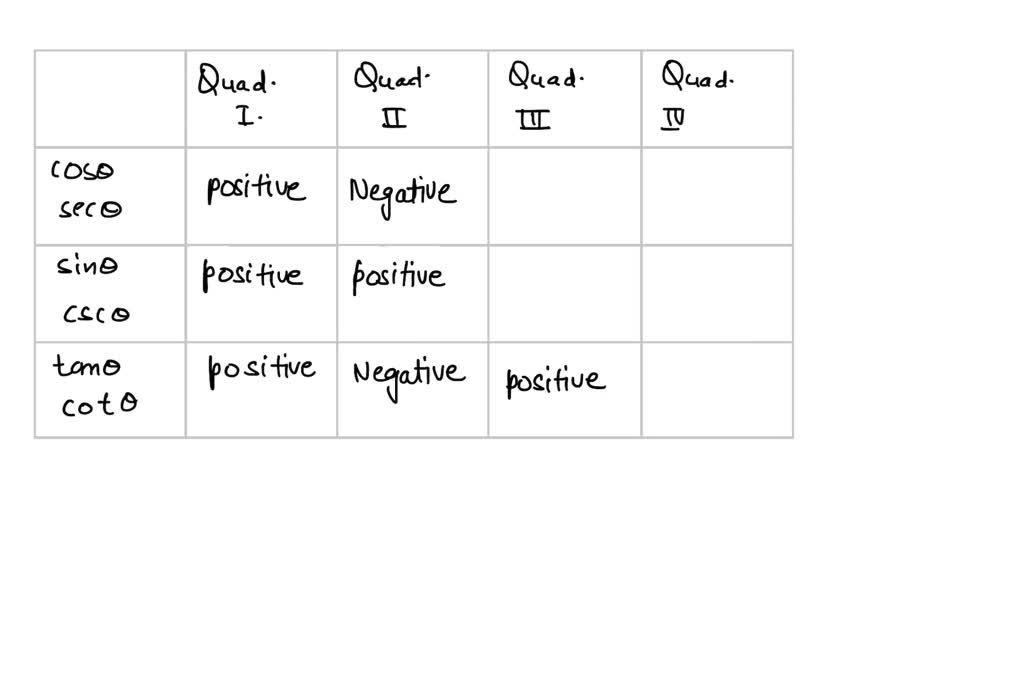
‘C’ for cosine: In the fourth quadrant, only the cosine function has positive value Formulas How to Find a Reference Angle ‘T’ for tangent: In the third quadrant, tangent and cotangent have positive values
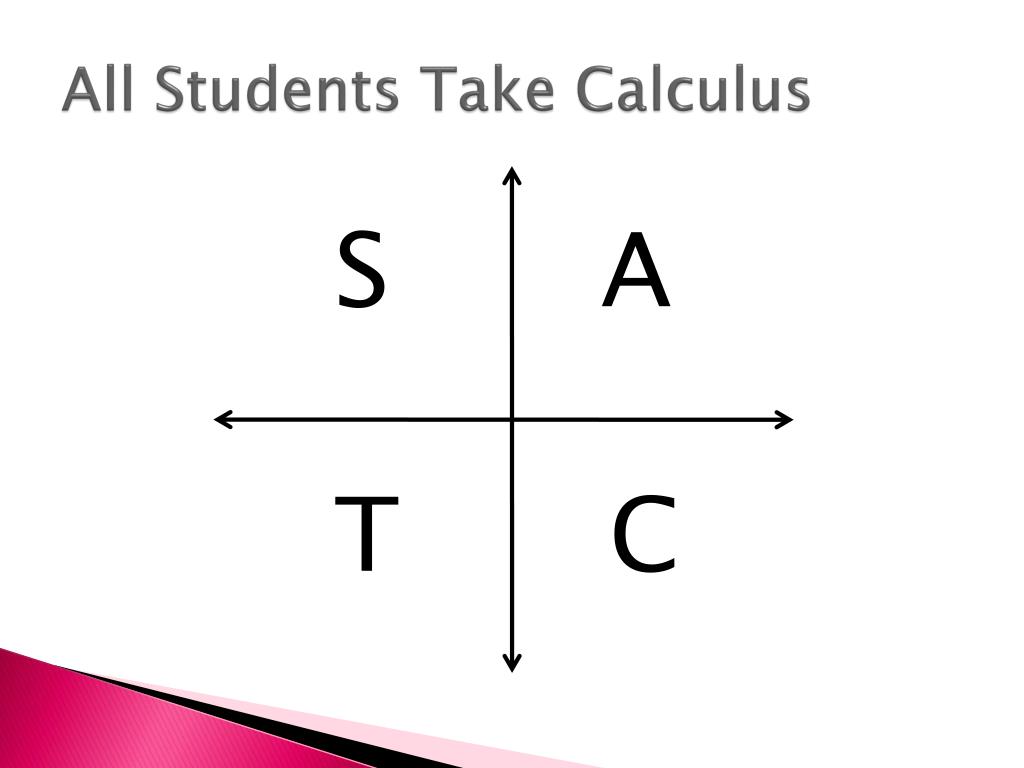
‘S’ for sine: In the second quadrant, only the sine function has positive value ‘A’ for all: In the first quadrant, all functions have positive value The only thing that varies is the sign.įollow the mnemonic rule: ‘ Add Sugar To Coffee’ or ‘ All Students Take Calculus’ to remember when these functions have positive values. Normally, the four trigonometric functions: sine, cosine, tangent, and cotangent give the same value for an angle and its reference angle. The numbering starts from the upper right one, the first quadrant, where both coordinates are positive as we continue to move in the anticlockwise direction. The two axes, x, and y divide the plane into four quadrants, named I, II, III, and IV. Reference Angles and Trigonometric Functions Looking at the picture above, every angle is measured from the positive part of the x-axis to its terminal side by traveling in a counterclockwise direction. A reference angle always uses an x-axis as its frame of reference. Their value is always between 0 and 90° when measured in degrees or 0 and π/2 when measured in radians.

The reference angle is used for simplifying the calculations related to trigonometric functions with different angles.


 0 kommentar(er)
0 kommentar(er)
